Dynamic Programming
Dynamic programming is a powerful algorithmic technique that I find extremely valuable in solving complex problems efficiently. When faced with optimization problems that can be broken down into overlapping subproblems, dynamic programming shines by storing and reusing solutions to these subproblems. This approach helps me avoid redundant calculations, making it a go-to method for enhancing the speed and efficiency of my problem-solving process.
One key concept in dynamic programming is the idea of memoization, where I store previously computed results and refer back to them when needed instead of recomputing. By maintaining a table or array to store these results, I can optimize time complexity significantly, especially in scenarios where recalculating values would lead to exponential time complexity.
Another essential aspect to grasp is the difference between top-down and bottom-up approaches in dynamic programming. While top-down involves breaking down the main problem into smaller subproblems and solving them recursively, bottom-up starts from the simplest subproblems and works its way up to the main problem. Understanding when to apply each method based on the nature of the given problem is crucial for effectively implementing dynamic programming solutions.

What is Dynamic Programming?
Dynamic Programming, often abbreviated as DP, is a powerful algorithmic technique used to solve complex problems by breaking them down into simpler subproblems. This method efficiently solves problems by storing the results of subproblems and reusing them when needed, ultimately leading to optimized solutions.
At its core, Dynamic Programming relies on two key principles: optimal substructure and overlapping subproblems. Optimal substructure means that an optimal solution can be constructed from optimal solutions of its subproblems. Overlapping subproblems refer to situations where the same subproblem is encountered multiple times during the execution of an algorithm.
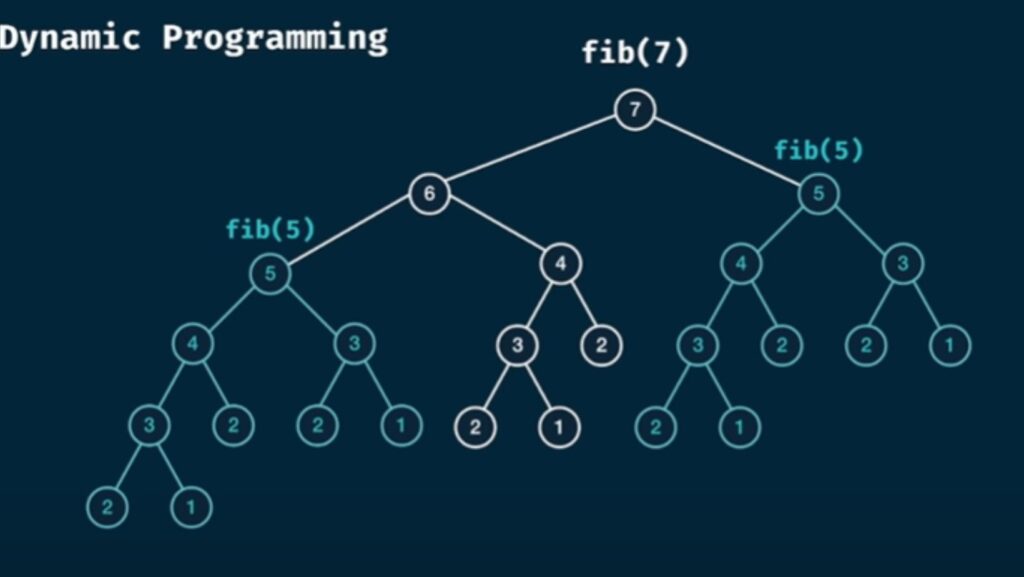
One famous example that illustrates the concept of Dynamic Programming is the Fibonacci sequence problem. By using DP techniques to store intermediate results, we can avoid redundant calculations and significantly improve the efficiency of computing Fibonacci numbers for large values.
In real-world applications, Dynamic Programming finds extensive use in various fields such as computer science, economics, biology, and more. It’s commonly employed in tasks like sequence alignment, resource allocation, scheduling problems, and other optimization challenges where breaking down complex challenges into smaller manageable parts leads to more efficient solutions.
By mastering Dynamic Programming techniques and understanding its fundamental principles, developers can tackle intricate problems with greater ease and achieve optimized outcomes across a wide range of domains.

Key Concepts in Dynamic Programming
Dynamic programming is a powerful algorithmic technique that involves breaking down complex problems into simpler subproblems to solve them more efficiently. Here are some key concepts to grasp the essence of dynamic programming:
Optimal Substructure
- At the core of dynamic programming lies the concept of optimal substructure, where an optimal solution can be constructed from optimal solutions of its subproblems.
- By identifying and solving these subproblems independently, we can avoid redundant calculations and improve overall efficiency.
Overlapping Subproblems
- Another crucial concept in dynamic programming is overlapping subproblems, where the same subproblem is solved multiple times.
- To address this inefficiency, dynamic programming stores the results of subproblems in a data structure (usually an array or a hash table) for easy retrieval when needed again.
Memoization
- Memoization is a technique used to store and reuse solutions to overlapping subproblems.
- By caching computed results, subsequent recursive calls can directly fetch the precomputed values rather than recalculating them, reducing time complexity significantly.
Tabulation
- In contrast to memoization, tabulation is a bottom-up approach where solutions to smaller subproblems are iteratively computed first before moving on to larger ones.
- This method often uses arrays or matrices to store intermediate results and build up towards solving the main problem.
Understanding these foundational concepts will set you on the right path for effectively applying dynamic programming strategies to tackle intricate computational challenges. Stay tuned for practical examples and applications in our forthcoming sections!